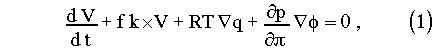
Presently the Canadian Meteorological Centre operationally runs two models: a global spectral model for medium-range forecasting [Ritchie (1994)] and a variable-resolution regional finite-element model for regional forecasting [Mailhot (1994)]. This strategy is similar to that used at a number of national centers. There is however an associated practical difficulty entailing considerable personnel overhead, namely that there are two systems to maintain, improve, optimize and adapt to new computers. This motivates the development of a single highly-efficient model, that can be reconfigured at run time to either run globally at uniform-resolution (with possibly degraded resolution in the hemisphere of least interest to the center), or to run with variable resolution over a global domain such that high resolution is focused over any area of interest, and thereby meet the needs of both medium-range global and short-range regional forecasting with a single model. The main idea behind this thrust is that the finite-element method permits variable resolution in a natural way, and a focusing of resolution over an area of interest. This offers an efficient and simple solution to the nesting problem.
To demonstrate the potential of this strategy, a shallow-water global variable-resolution prototype using highly-efficient numerical techniques has been developed [Côté (1993)] that uses an arbitrarily-rotated latitude-longitude mesh. In this way a high-resolution subdomain can be focused on any geographical area of interest, be it tropical or extra-tropical, making it a more flexible strategy than the operational finite-element regional model, which is limited to extra-tropical applications. This shallow-water model has been successfully integrated on a variety of meshes right down to the mesoscale (with 250 m resolution over a 100 km x 100 km subdomain). An important conclusion is that the overhead associated with using a model of global extent for short-range forecasting, even at the meso-[[gamma]] scale, is relatively small: more than half of the total number of meshpoints are on the uniform-resolution area of interest, and the overhead of using variable resolution outside this area is consequently comparable to that of the sponge regions of one-way interacting models.
In the present work we extend the formulation to three dimensions. To maintain the validity of the model at the mesoscale, the formulation uses the non-hydrostatic Euler equations, with a switch to revert to the hydrostatic primitive equations for large scale applications where the hydrostatic assumption is valid. To this end a pressure-type hybrid vertical coordinate is adopted as proposed in Laprise (1992).
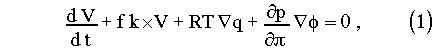
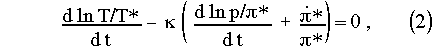
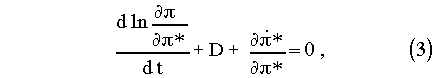
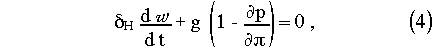
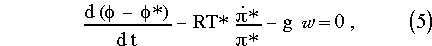
where the symbols have their usual meaning or are defined below. [[phi]]* and T* have been introduced in anticipation of semi-implicit time differencing. dH is a switch (0/1) for the non-hydrostatic terms. When dH is 0 eq. (5) decouples and we have the usual hydrostatic set. Hydrostatic pressure [[pi]] is a pressure field in hydrostatic balance such that
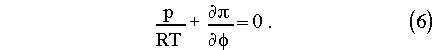
To completely specify [[pi]] we impose the auxiliary condition [[pi]]T = pT, i.e. pressure and hydrostatic pressure are identical at the model top. The vertical coordinate [[pi]]* is related to [[pi]] by,
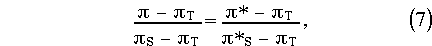
where subscript "s" refers to values at the earth's surface.
The boundary conditions are, as usual, no motion across the top and the bottom where the top is a constant pressure level. Thus
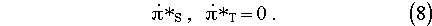
The implicit semi-Lagrangian time differencing transforms each of the prognostic equations in the following way
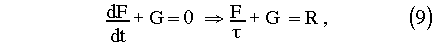
where F and G are the unknowns that we wish to forecast and R subsumes everything that is known. The time-discretized equations form a set of coupled non-linear partial differential equations that are solved by a process of linearization/iteration. First the variables are split, so
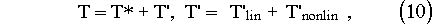
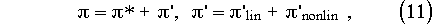
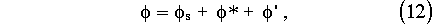
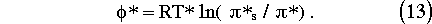
Next the non-linear contributions to the equations are evaluated using the most recent values and put on the right-hand sides, leading to an elliptic boundary value problem for the variable

Thus
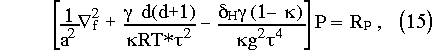
where --f2 is a Laplacian modified by the Coriolis parameter, d = [[pi]]*[[partialdiff]]/[[partialdiff]][[pi]]* and
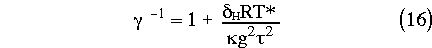
After solving (15) the other variables are updated by backsubstitution. The horizontal discretization proceeds as in Côté (1993) and the vertical discretization is similar to that of Tanguay (1989): both are based on the principle of discretization of the equations followed by an algebraic elimination between the discretized equations to produce the discretization of (15).
Key ingredients of this strategy include the use of: (i) the non-hydrostatic Euler equations (with a switch to revert to the hydrostatic primitive equations) to maintain the model's validity right down to the meso-[[gamma]] scales; (ii) a semi-implicit time scheme to overcome the stability limitations imposed by the fastest-moving acoustic and gravity-wave terms that carry negligibly-small energy; (iii) a semi-Lagrangian treatment of advection to overcome the stability limitations encountered in Eulerian schemes due to the convergence of the meridians and to strong jets; (iv) a finite-element spatial discretization to provide a robust way of achieving variable resolution; and (v) an arbitrarily-rotated latitude-longitude mesh to focus resolution on any part of the globe, be it mid-latitudinal or tropical.
The formulation and coding of our nonhydrostatic variable-resolution global Euler equation model is complete, and testing is underway. Preliminary results are encouraging.
Laprise, R., 1992: The Euler equations of motion with hydrostatic pressure as independent variable. Mon. Wea. Rev., 120, 197-207.
Mailhot, J., R. Sarrazin, B. Bilodeau, N. Brunet, A. Methot, G. Pellerin, C. Chouinard, L. Garand, C. Girard and R. Hogue:, 1995: Changes to the Canadian regional forecast system - description and evaluation of the 50 km version. Atmosphere-Ocean, (submitted)
Ritchie, H. and C. Beaudoin, 1994: Approximations and sensitivity experiments with a baroclinic semi-Lagrangian spectral model. Mon. Wea. Rev. (to appear).
Tanguay, M., A. Simard, and A. Staniforth, 1989: A three-dimensional semi-Lagrangian scheme for the Canadian regional finite-element forecast model. Mon. Wea. Rev., 117, 1861-1871.