A GENERALIZED FAMILY OF SCHEMES THAT ELIMINATE THE SPURIOUS RESONANT
RESPONSE OF SEMI-LAGRANGIAN SCHEMES TO OROGRAPHIC FORCING
Jean Côté, Sylvie Gravel and Andrew Staniforth
Recherche en prévision numérique
Service de l'environnement atmosphérique
2121 Route Transcanadienne, porte 500
Dorval, Québec
CANADA H9P 1J3
March 1995
Submitted to Monthly Weather Review
ABSTRACT
The one-parameter three-time-level family of
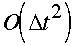 -accurate
schemes, introduced in Rivest et al. (1994) to address the problem of the
spurious resonant response of semi-implicit semi-Lagrangian schemes at large
Courant number, has been generalized to a two-parameter family by introducing
the possibility of evaluating total derivatives using an additional time level.
The merits of different members of this family based on both theory and results
are assessed. The additional degree of freedom might be expected a priori to
permit a reduction of the time truncation errors while still maintaining
stability and avoiding spurious resonance. Resonance, stability and truncation
error analyses for the proposed generalized family of schemes are given. The
sub-family that is formally
-accurate
schemes, introduced in Rivest et al. (1994) to address the problem of the
spurious resonant response of semi-implicit semi-Lagrangian schemes at large
Courant number, has been generalized to a two-parameter family by introducing
the possibility of evaluating total derivatives using an additional time level.
The merits of different members of this family based on both theory and results
are assessed. The additional degree of freedom might be expected a priori to
permit a reduction of the time truncation errors while still maintaining
stability and avoiding spurious resonance. Resonance, stability and truncation
error analyses for the proposed generalized family of schemes are given. The
sub-family that is formally
 -accurate
is unfortunately unstable for gravity modes. Sample integrations for various
members of the generalized family are shown. Results are consistent with
theory, and stable non-resonant forecasts at large Courant number are possible
for a fairly broad choice of values of the two free parameters. Of the two
methods proposed in Rivest et al. (1994) for computing trajectories, the one
using a piecewise-defined trajectory is to be preferred to that using a single
great-circle arc, since it is more accurate at large timestep for some members
of the generalized family.
-accurate
is unfortunately unstable for gravity modes. Sample integrations for various
members of the generalized family are shown. Results are consistent with
theory, and stable non-resonant forecasts at large Courant number are possible
for a fairly broad choice of values of the two free parameters. Of the two
methods proposed in Rivest et al. (1994) for computing trajectories, the one
using a piecewise-defined trajectory is to be preferred to that using a single
great-circle arc, since it is more accurate at large timestep for some members
of the generalized family.
Since Robert et al. (1985) first demonstrated a semi-implicit semi-Lagrangian
discretization of the hydrostatic primitive equations, this method has found
increasing favor at weather-forecasting and climate centers throughout the
world (e.g., Bates et al. 1993; McDonald and Haugen 1992; Purser and Leslie
1994; Ritchie and Beaudoin 1994; Ritchie et al. 1995; Tanguay et al. 1989;
Williamson and Olson 1994).
Although it has been known for some time (Kaas 1987; Coiffier et al. 1987;
Staniforth & Côté 1991; Tanguay et al. 1992) that
semi-implicit semi-Lagrangian schemes can experience difficulties at high
Courant number in the presence of orography, it is only recently that this
problem has been elucidated. In Rivest et al. (1994), hereafter referred to as
RSR94, its source was clearly identified and a solution proposed in a
two-time-level context. It consists of off-centering the
semi-implicitly-treated terms along the trajectory, and Rivest & Staniforth
(1995) have proposed a possible retrofit scheme for three-time-level-based
centered schemes. Héreil & Laprise (1995) have recently extended
the RSR94 analysis to the semi-implicit semi-Lagrangian discretization of
Tanguay et al. (1990) of the non-hydrostatic Euler equations.
The goals of the present study are to present a generalization of the RSR94
family of schemes, and to assess the merits of different members of this family
based on both theory and results.
The linearized one-dimensional shallow-water equations after a three-time-level
semi-implicit semi-Lagrangian discretization may be written as (cf. RSR94):
 ,
(2.1)
,
(2.1)
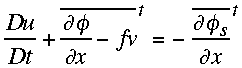 ,
(2.2)
,
(2.2)
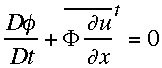 ,
(2.3)
,
(2.3)
where
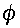 and
and
 are respectively the fluid depth and orographic height multiplied by
are respectively the fluid depth and orographic height multiplied by
 ,
the other symbols have their usual meaning, and for the generalized
family of schemes introduced here:
,
the other symbols have their usual meaning, and for the generalized
family of schemes introduced here:
 ,
(2.4)
,
(2.4)
 ,
(2.5)
,
(2.5)
 .
(2.6)
.
(2.6)
The basic-state quantities
 and
and
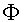 are assumed non-zero, and the orographic geopotential
are assumed non-zero, and the orographic geopotential
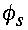 is both non-zero and time invariant. The linearized equations before
discretization may be recovered by redefining
is both non-zero and time invariant. The linearized equations before
discretization may be recovered by redefining
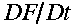 and
and
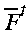 as:
as:
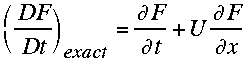 ,
(2.7)
,
(2.7)
 .
(2.8)
.
(2.8)
The above 2-parameter (
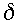 ,
, )
family of schemes is the most general
)
family of schemes is the most general
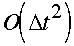 -accurate
scheme based on three time levels, and is a generalization of the 1-parameter (
-accurate
scheme based on three time levels, and is a generalization of the 1-parameter (
 )
family presented in RSR94. The parameter
)
family presented in RSR94. The parameter
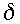 here is exactly as in RSR94. It was introduced there to decenter the
2-time-level Crank-Nicolson semi-implicit semi-Lagrangian discretization, and
thereby address the problem of spurious orogrophically-induced resonance by
introducing a third time level to evaluate the time-averaged contributions
along the trajectory. A further new parameter
here is exactly as in RSR94. It was introduced there to decenter the
2-time-level Crank-Nicolson semi-implicit semi-Lagrangian discretization, and
thereby address the problem of spurious orogrophically-induced resonance by
introducing a third time level to evaluate the time-averaged contributions
along the trajectory. A further new parameter
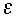 has been added here. It optionally introduces the use of a third time level
in the evaluation of the time derivatives along the trajectory. This
additional degree of freedom might be expected a priori to permit an
improvement to the RSR94 family of schemes by reducing the time truncation
errors [possibly to
has been added here. It optionally introduces the use of a third time level
in the evaluation of the time derivatives along the trajectory. This
additional degree of freedom might be expected a priori to permit an
improvement to the RSR94 family of schemes by reducing the time truncation
errors [possibly to
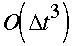 ]
while still maintaining stability and avoiding spurious resonance. This is
discussed further later. Special cases of the above generalized scheme for
particular values of
]
while still maintaining stability and avoiding spurious resonance. This is
discussed further later. Special cases of the above generalized scheme for
particular values of
 and
and
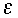 are summarized in Table 1.
are summarized in Table 1.
d [[eps Scheme
ilon]
]
0 0 Crank-Nicolson using time levels t and t-[[Delta]]t

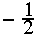 Crank-Nicolson using time levels t and
t-2[[Delta]]t
d 0 General RSR94 1-parameter (d) scheme
Crank-Nicolson using time levels t and
t-2[[Delta]]t
d 0 General RSR94 1-parameter (d) scheme
 0 Particular RSR94 scheme, for which results were
shown
0 Particular RSR94 scheme, for which results were
shown

 Backward implicit
Backward implicit
Table
1: Particular cases of the generalized scheme as a function of
 and
and
 .
The complete solution to the linear system (2.1)-(2.3) can be written as the
sum of free and forced modes:
.
The complete solution to the linear system (2.1)-(2.3) can be written as the
sum of free and forced modes:
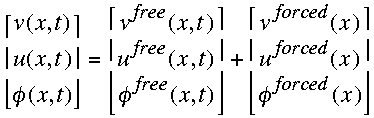 .
(2.7)
.
(2.7)
The free solutions satisfy (2.1)-(2.3) with the forcing
 set identically to zero. Letting
set identically to zero. Letting
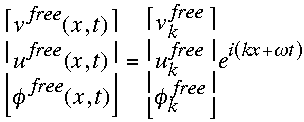 ,
(2.8)
,
(2.8)
each free mode (there are three for each wavenumber) then satisfies
 ,
(2.9)
,
(2.9)
where
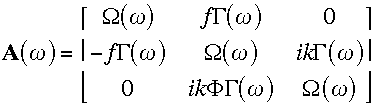 ,
(2.10)
,
(2.10)
 ,
(2.11)
,
(2.11)
 ,
(2.12)
,
(2.12)
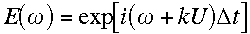 ,
(2.13)
,
(2.13)
and exact interpolation has been assumed. Setting
 ,
(2.14)
,
(2.14)
then gives the dispersion relation for
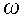 .
Note that for the exact solution of the linearized equations (with no
discretization), (2.11)-(2.12) may be replaced by the definitions
.
Note that for the exact solution of the linearized equations (with no
discretization), (2.11)-(2.12) may be replaced by the definitions
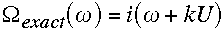 ,
(2.15)
,
(2.15)
 ,
(2.16)
,
(2.16)
and the usual (free) Rossby and gravity-wave dispersion relations then result
from (2.14):
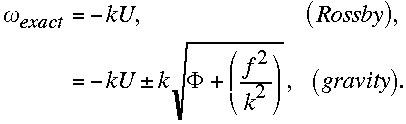 (2.17)
(2.17)
The forced solutions satisfy (2.1)-(2.3) in the absence of any time
variation (
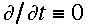 ),
and may be Fourier decomposed as
),
and may be Fourier decomposed as
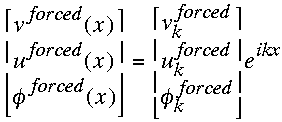 .
(2.18)
.
(2.18)
They then satisfy
 .
(2.19)
.
(2.19)
Note that for the exact solution of the linearized equations (with no
discretization),
 simplifies to
simplifies to
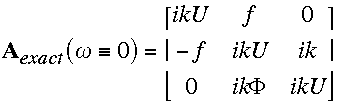 ,
(2.20)
,
(2.20)
(cf. RSR94). Physical resonance then occurs when the determinant of
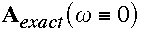 vanishes, i.e. when
vanishes, i.e. when
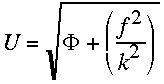 ,
(2.21)
,
(2.21)
which, as discussed in RSR94, corresponds to supersonic flow and is unlikely to
occur in a shallow-water model representative of the atmosphere at 500 hPa.
The existence or not of resonance is determined from (2.19), and a scheme's
stability from the solutions of the dispersion relation (2.14). Note that the
matrix
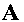 defined by (2.10) plays a determining role for both resonance and stability.
These latter are respectively discussed in the following two sub-sections.
defined by (2.10) plays a determining role for both resonance and stability.
These latter are respectively discussed in the following two sub-sections.
For the discretized linear equations, whenever
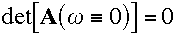 ,
(2.22)
,
(2.22)
the stationary forced gravity modes determined by (2.19) are resonant, and
these resonances may be spurious (RSR94). This leads to the following two
quadratic equations that govern the resonance of the stationary forced gravity
solutions:
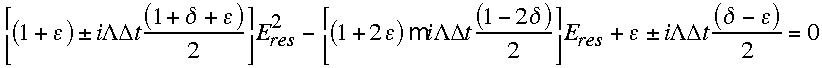 ,
(2.23)
,
(2.23)
where
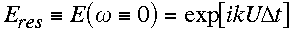 ,
(2.24)
,
(2.24)
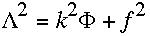 .
(2.25)
.
(2.25)
Since
 is real by definition, resonance is only possible if
is real by definition, resonance is only possible if
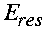 lies on the unit circle, i.e. if
lies on the unit circle, i.e. if
 .
(2.26)
.
(2.26)
For the special case
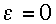 ,
the conditions (2.23) for resonance in the present 2-parameter (
,
the conditions (2.23) for resonance in the present 2-parameter (
 )
family of schemes reduce to (15) of RSR94 for their 1-parameter (
)
family of schemes reduce to (15) of RSR94 for their 1-parameter (
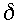 )
family. The further special case
)
family. The further special case
 (cf. Table 1), corresponds to the conditions (9) of RSR94 for the spurious
resonance of centered 2-time-level semi-implicit semi-Lagrangian schemes. As
discussed in RSR94, spurious resonance occurs for certain combinations of large
Courant number and nondimensional wavenumbers of the orographic forcing, and
can be avoided by suitably off-centering the time discretization along the
trajectory. In the present study this is controlled by the
(cf. Table 1), corresponds to the conditions (9) of RSR94 for the spurious
resonance of centered 2-time-level semi-implicit semi-Lagrangian schemes. As
discussed in RSR94, spurious resonance occurs for certain combinations of large
Courant number and nondimensional wavenumbers of the orographic forcing, and
can be avoided by suitably off-centering the time discretization along the
trajectory. In the present study this is controlled by the
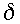 and
and
 parameters.
parameters.
Summarizing, any of the schemes considered here will be non-resonant provided
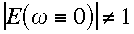 .
They may not however necessarily be stable, and this aspect of the
discretization is examined in the following sub-section.
.
They may not however necessarily be stable, and this aspect of the
discretization is examined in the following sub-section.
Stability is determined from the dispersion relation obtained by solving
(2.14). Thus
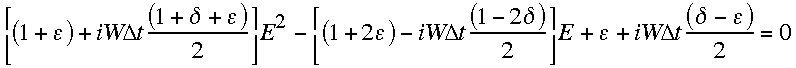 ,
(2.27)
,
(2.27)
where
 ,
(2.28)
,
(2.28)
 ,
(2.29)
,
(2.29)
and the scheme is stable provided
 .
(2.30)
.
(2.30)
Note that (2.27) can be identified with the dispersion relation that would
result from applying the generalized family of schemes of the present study to
an oscillation equation, yielding the discretization
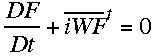 ,
(2.31)
,
(2.31)
where
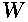 is real. This is equivalent to having performed a decomposition in terms of
the eigen-functions of the matrix
is real. This is equivalent to having performed a decomposition in terms of
the eigen-functions of the matrix
 .
The leading-order term of the truncation error (placed on the right-hand side
of 2.31) is
.
The leading-order term of the truncation error (placed on the right-hand side
of 2.31) is
 .
(2.32)
.
(2.32)
For the quadratic associated with the Rossby modes (for which
 ),
(2.27) factors easily and
),
(2.27) factors easily and
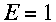 or
or
 .
The first root corresponds to the physical Rossby mode and it is stable since
it satisfies (2.30). The other root corresponds to a computational Rossby mode
(introduced by discretizing a 1st-order-in-time equation over three time
levels), and it will satisfy (2.30) and be stable provided
.
The first root corresponds to the physical Rossby mode and it is stable since
it satisfies (2.30). The other root corresponds to a computational Rossby mode
(introduced by discretizing a 1st-order-in-time equation over three time
levels), and it will satisfy (2.30) and be stable provided
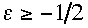 .
Now
.
Now
 corresponds to a centered three-time-level discretization, and this value for
corresponds to a centered three-time-level discretization, and this value for
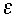 must be excluded since (see above and RSR94) the stationary forced gravity
modes would suffer from spurious resonance. Although satisfaction of the
strict inequality
must be excluded since (see above and RSR94) the stationary forced gravity
modes would suffer from spurious resonance. Although satisfaction of the
strict inequality
 is sufficient to stabilize the computational Rossby mode,
is sufficient to stabilize the computational Rossby mode,
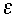 should be positive, otherwise it will have the undesirable property of changing
the sign of this computational mode at alternate timesteps (timestep
decoupling).
should be positive, otherwise it will have the undesirable property of changing
the sign of this computational mode at alternate timesteps (timestep
decoupling).
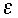 should not only be positive but small to ensure adequate damping of this
computational mode during the integration.
should not only be positive but small to ensure adequate damping of this
computational mode during the integration.
For the quadratic associated with the gravity modes (for which
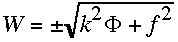 ),
(2.27) does not factor easily. It is nevertheless possible to get some insight
into the influence of
),
(2.27) does not factor easily. It is nevertheless possible to get some insight
into the influence of
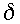 and
and
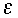 on the stability of the free gravity solutions by solving (2.27) asymptotically
for
on the stability of the free gravity solutions by solving (2.27) asymptotically
for
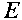 for the physical mode when
for the physical mode when
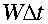 is small. Taking its modulus then gives
is small. Taking its modulus then gives
 .
(2.33)
.
(2.33)
From above, since
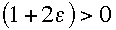 for stability of the computational Rossby solution, it is necessary to take
for stability of the computational Rossby solution, it is necessary to take
 ,
(2.34)
,
(2.34)
in order to both satisfy the stability condition (2.30) and to also remain off
resonance. This is a necessary condition for stability. From (2.32), it has
the further consequence that the only
 -accurate member of the present generalized family of three-time-level schemes
(i.e.
-accurate member of the present generalized family of three-time-level schemes
(i.e.
 )
is unstable and therefore inadmissible. This is unfortunate. By numerically
solving (2.27) when
)
is unstable and therefore inadmissible. This is unfortunate. By numerically
solving (2.27) when
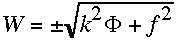 for a broad range of values of the parameters
for a broad range of values of the parameters
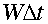 ,
,
 ,
and
,
and
 ,
it is found that the valid domain for remaining both stable and off resonance
is
,
it is found that the valid domain for remaining both stable and off resonance
is
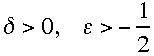 ,
(2.35)
,
(2.35)
as suggested by the above analysis.
Summarizing, it is advisable to choose
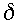 and
and
 from the more restricted domain
from the more restricted domain
 ,
(2.36)
,
(2.36)
to avoid having a time-decoupled computational Rossby mode. It is also
advisable to use the smallest-possible values of
 and
and
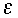 (consistent with being adequately off-resonance), to respectively minimize the
truncation errors (see 2.32) and to maximally damp the computational Rossby
mode.
(consistent with being adequately off-resonance), to respectively minimize the
truncation errors (see 2.32) and to maximally damp the computational Rossby
mode.
The variable-resolution global shallow-water model described in
Côté et al. (1993) has been modified to include the present
generalized family of semi-implicit semi-Lagrangian time schemes. To evaluate
the proposed family of schemes and to provide some guidance on the choice of
the values for the parameters
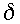 and
and
 ,
the methodology introduced in RSR94 is adopted. The grid configuration and the
model orography used here are as depicted in their Figs. 4 and 5. The grid has
a uniform (
,
the methodology introduced in RSR94 is adopted. The grid configuration and the
model orography used here are as depicted in their Figs. 4 and 5. The grid has
a uniform (
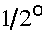 )
resolution window over N. America, and the orography is zero everywhere outside
this window. The experiments consist of 48-h forecasts initiated from the
500hPa height and wind analyses of 1200 UTC 12 February 1979 after an
implicit-normal-mode initialization. The initialized geopotential used in all
of the described experiments is displayed in Fig. 6 of RSR94.
)
resolution window over N. America, and the orography is zero everywhere outside
this window. The experiments consist of 48-h forecasts initiated from the
500hPa height and wind analyses of 1200 UTC 12 February 1979 after an
implicit-normal-mode initialization. The initialized geopotential used in all
of the described experiments is displayed in Fig. 6 of RSR94.
Two methods for computing trajectories were described in RSR94, and for both of
these the upstream point at time
 is obtained as in Côté et al. (1993) using winds extrapolated
forward from those at ess the problem of the spurious resonance of
semi-implicit semi-Lagrangian schemes at large Courant number, has been
generalized to a two-parameter three-time-level family by introducing the
possibility of evaluating total derivatives using an additional time level of
information. The RSR94 family can be considered to be the limiting case of the
generalized family that maximally simplifies the evaluation (using a
two-time-level difference) of the total derivatives. The other limiting case
is the "backward-implicit" scheme, where maximum simplification of the
evaluation (entirely at the arrival point) of the other terms occurs, and where
an additional (third) time level is employed to evaluate the total derivatives.
It has the virtues that the only upstream evaluations required are those
associated with the total derivatives, and that it does not require derivative
terms such as
is obtained as in Côté et al. (1993) using winds extrapolated
forward from those at ess the problem of the spurious resonance of
semi-implicit semi-Lagrangian schemes at large Courant number, has been
generalized to a two-parameter three-time-level family by introducing the
possibility of evaluating total derivatives using an additional time level of
information. The RSR94 family can be considered to be the limiting case of the
generalized family that maximally simplifies the evaluation (using a
two-time-level difference) of the total derivatives. The other limiting case
is the "backward-implicit" scheme, where maximum simplification of the
evaluation (entirely at the arrival point) of the other terms occurs, and where
an additional (third) time level is employed to evaluate the total derivatives.
It has the virtues that the only upstream evaluations required are those
associated with the total derivatives, and that it does not require derivative
terms such as
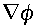 and
and
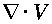 to be evaluated at any time other than the present one (which is done
implicitly and only at arrival meshpoints). Both of these limiting cases are
off-centered discretizations, to avoid spurious resonance, and all schemes
examined are
to be evaluated at any time other than the present one (which is done
implicitly and only at arrival meshpoints). Both of these limiting cases are
off-centered discretizations, to avoid spurious resonance, and all schemes
examined are
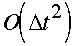 accurate.
accurate.
Resonance, stability and truncation-error analyses have been performed for the
proposed generalized family of schemes. Theory then leads to the following
conclusions:
a) to avoid instability and resonance the domain of validity for the parameters
is (
 ,
,
 );
);
b) it is advisable to choose
 and
and
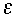 from the more restricted domain (
from the more restricted domain (
 ,
,
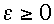 ),
to avoid having a time-decoupled computational Rossby mode;
),
to avoid having a time-decoupled computational Rossby mode;
c) it is also advisable to use the smallest-possible values of
 and
and
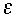 (consistent with being adequately off resonance), to respectively minimize the
truncation errors and to maximally damp the computational Rossby mode;
(consistent with being adequately off resonance), to respectively minimize the
truncation errors and to maximally damp the computational Rossby mode;
d) the backward-implicit scheme has twice the damping rate of the RSR94 scheme,
even though they both have the same leading-order truncation error; and
e) although there is a sub-family of the generalized family of schemes that is
formally
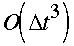 -accurate
(
-accurate
(
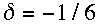 ,
,
 free), it is unstable for the gravity modes; this is unfortunate; starting from
a stable-but-resonant centered two-time-level scheme (
free), it is unstable for the gravity modes; this is unfortunate; starting from
a stable-but-resonant centered two-time-level scheme (
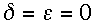 ),
a degree of freedom can be added to address resonance (by using an additional
time level and thereby decentering either the evaluation of the total
derivatives or the other terms), but adding a further degree of freedom (while
still only using three time levels) does not permit increasing accuracy to
),
a degree of freedom can be added to address resonance (by using an additional
time level and thereby decentering either the evaluation of the total
derivatives or the other terms), but adding a further degree of freedom (while
still only using three time levels) does not permit increasing accuracy to
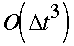 .
.
Sample integrations for various members of the generalized family were
performed. It was found that the results were consistent with the theory, and
that stable non-resonant forecasts at large Courant number are possible for a
fairly-broad choice of values for the
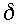 and
and
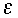 parameters. Within the RSR94 family of schemes, the scheme (
parameters. Within the RSR94 family of schemes, the scheme (
 )
for which results were shown in RSR94 is a good choice but not an optimal one.
A smaller value of
)
for which results were shown in RSR94 is a good choice but not an optimal one.
A smaller value of
 than 1/2, but no smaller than 1/6, can reduce the leading-order term for the
truncation error by as much as a factor of 2 (see 2.32) and the damping rate by
as much as a factor of 3 (see 2.33), while still acceptably controlling
resonance. Finally, it was found that while either of the two methods
presented in RSR94 for computing the trajectories is acceptable for their
scheme, only one of them is acceptable at large timestep for some members of
the generalized family. The method that computes the trajectory in a piecewise
fashion is therefore to be preferred to the one that uses a single great-circle
trajectory.
than 1/2, but no smaller than 1/6, can reduce the leading-order term for the
truncation error by as much as a factor of 2 (see 2.32) and the damping rate by
as much as a factor of 3 (see 2.33), while still acceptably controlling
resonance. Finally, it was found that while either of the two methods
presented in RSR94 for computing the trajectories is acceptable for their
scheme, only one of them is acceptable at large timestep for some members of
the generalized family. The method that computes the trajectory in a piecewise
fashion is therefore to be preferred to the one that uses a single great-circle
trajectory.
Bates, J.R., S. Moorthi, and R.W. Higgins, 1993: A global multilevel
atmospheric model using a vector semi-Lagrangian finite-difference scheme. Part
I: Adiabatic formulation. Mon. Wea. Rev., 121, 244-263.
Coiffier, J., P. Chapelet, and N. Marie, 1987: Study of various
quasi-Lagrangian techniques for numerical models. Proceedings of ECMWF
Workshop on Techniques for Horizontal Discretization in Numerical Weather
Prediction Models, 19-46, European Centre for Medium-range Weather Forecasts,
Shinfield Park, Reading, U.K., 377 pp.
Côté, J., M. Roch, A. Staniforth, andnbsp;L. Fillion,
1993: A variable-resolution semi-Lagrangian finite-element global model of
the shallow-water equations. Mon. Wea. Rev., 121, 231-243.
Héreil, P., and R. Laprise, 1995: Sensitivity of internal gravity wave
solutions to the timestep of a semi-implicit semi-Lagrangian nonhydrostatic
model. Mon. Wea. Rev., 123, submitted.
Kaas, E., 1987: The construction of and tests with a multi-level,
semi-Lagrangian and semi-implicit limited area model. Diploma thesis,
Geophysics Institute, Copenhagen University, Copenhagen, Denmark, 117 pp.
McDonald, A., and J.E. Haugen, 1992: A two-time-level, three-dimensional
semi-Lagrangian, semi-implicit, limited-area gridpoint model of the primitive
equations. Mon. Wea. Rev., 120, 2603-2621.
Purser, R.J., and L.M. Leslie, 1994: An efficient semi-Lagrangian scheme using
third-order semi-implicit time integration and forward trajectories. Mon.
Wea. Rev., 122, 745-756.
Ritchie, H., and C. Beaudoin, 1994: Approximations and sensitivity experiments
with a baroclinic semi-Lagrangian spectral model. Mon. Wea. Rev.,
122, 2391-2399.
Ritchie, H., C. Temperton, A. Simmons, M. Hortal, T. Davies, D. Dent, and M.
Hamrud, 1995: Implementation of the semi-Lagrangian method in a
high-resolution version of the ECMWF forecast model. Mon. Wea. Rev.,
123, 489-514.
Rivest, C., A. Staniforth, and A. Robert, 1994: Spurious resonant response of
semi-Lagrangian discretizations to orographic forcing: Diagnosis and solution.
Mon. Wea. Rev., 122, 366-376.
Rivest, C., and A. Staniforth, 1995: Modifying the conventional
three-time-level semi-implicit semi-Lagrangian scheme to eliminate
orographically-induced spurious resonance. Atmos.-Ocean, 33, in
press.
Robert, A., T.L. Yee, and H. Ritchie, 1985: A semi-Lagrangian and semi-implicit
numerical integration scheme for multilevel atmospheric models. Mon. Wea.
Rev., 113, 388-394.
Staniforth, A., and J. Côté, 1991: Semi-Lagrangian integration
schemes for atmospheric models - a review. Mon. Wea. Rev., 119,
2206-2223.
Tanguay, M., A. Simard, and A. Staniforth, 1989: A three-dimensional
semi-Lagrangian scheme for the Canadian regional finite-element forecast model.
Mon. Wea. Rev., 117, 1861-1871.
Tanguay, M., A. Robert, and R. Laprise, 1990: A semi-implicit semi-Lagrangian
fully compressible regional forecast model. Mon. Wea. Rev., 118,
1970-1980.
Tanguay, M., E. Yakimiw, H. Ritchie, and A. Robert, 1992: Advantages of spatial
averaging in semi-implicit semi-Lagrangian schemes. Mon. Wea. Rev.,
120, 124-130.
Williamson, D.L., and J.G. Olson, 1994: Climate simulations with a
semi-Lagrangian version of the NCAR CCM2. Mon. Wea. Rev., 122,
1594-1610.
Fig. 1 The geopotential height (dam) for the 48-h "control" forecast using a
centered 2-time-level scheme (
 )
with
)
with
 =10 min.
=10 min.
Fig. 2 As in Fig. 1, but for the
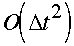 "backward-implicit" scheme (
"backward-implicit" scheme (
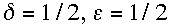 )
with
)
with
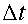 = 60 min.
= 60 min.
Fig. 3 As in Fig. 1, but for an uncentered RSR94 scheme (
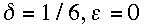 )
with
)
with
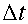 = 60 min.
= 60 min.
Fig. 4 The rms ge242E-02FULLGRD11700
ECRIT(63) 259-HU P 11700 18 0 136 100 1 GEF772 6021293122 1800 36 Z 1 0 1 0 R16 905056 3402
HU108.5409792456111 9374 -4.331157318724471E-05 9312 2.371501486475509E-02FULLGRD12000
ECRIT(63) 260-HU P 12000 18 0 136 100 1 GEF772 6021293122 1800 36 Z 1 0 1 0 R16 908461 3402
PN1381091462.329703 10893 95697.15881710777 7665 104664.2656081367FULLGRD0
ECRIT(63) 261-PN P 0 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 911866 3436
GZ745566433.0147386 9128 46677.31550861678 2507 57839.54471538262FULLGRD500
ECRIT(63) 262-GZ P 500 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 915316 3436
VT3785672.642612627 13135 229.1988389328281 9319 302.6429324226901FULLGRD850
ECRIT(63) 263-VT P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 918766 3436
HU70.64500518884305 8211 9.021589374571495E-05 9176 1.964754277741977E-02FULLGRD850
ECRIT(63) 264-HU P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 922216 3436
TT3773435.025580641 13135 229.0612968137486 9319 301.1204402953683FULLGRD850
ECRIT(63) 265-TT P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 925666 3436
ES83139.03365734413 12850 -26.48324409287316 8076 36.32389404153518FULLGRD850
ECRIT(63) 266-ES P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 929116 3436
TD3690295.991923297 8211 229.4158348383514 9176 295.2203248389047FULLGRD850
ECRIT(63) 267-TD P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 932566 3436
HR9670.441414632091 8076 3.581623693907646E-02 13135 11.37886305884168FULLGRD850
ECRIT(63) 268-HR P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 936016 3436
TW3835143.818062993 13135 242.1353481376335 9176 299.0810662873310FULLGRD850
ECRIT(63) 269-TW P 850 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 939466 3436
GZ14066479.41877066 10893 -3497.971588893279 12271 3373.372074382002FULLGRD1000
ECRIT(63) 270-GZ P 1000 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 942916 3436
UU146248.9370329119 136 -54.02499512503229 4665 68.35187930230893FULLGRD250
ECRIT(63) 271-UU P 250 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 946366 3436
VV10013.77712813014 7985 -70.66222955217516 10904 58.86112096349999FULLGRD250
ECRIT(63) 272-VV P 250 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 949816 3436
UV321411.3805455392 9615 0.3022683464920604 10141 81.72398946874964FULLGRD250
ECRIT(63) 273-UV P 250 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 953266 3436
DD-8.247046713814890E-04 13567 -8.124844453411657E-04 13554 1.062919422294302E-03FULLGRD500
ECRIT(63) 274-DD P 500 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 956716 3436
QQ0.7769327704211900 13531 -9.779306148793881E-04 13529 1.233133353781388E-03FULLGRD500
ECRIT(63) 275-QQ P 500 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 960166 3436
WW-92.43802585985704 13413 -5.620269452493929 13393 5.727755442957957FULLGRD700
ECRIT(63) 276-WW P 700 18 0 136 101 1 GEF772 6021293122 1800 36 Z 0 0 1 0 R16 963616 3436
THE TIME STEP 36 IS COMPLETED
THE TIME STEP 37 IS COMPLETED
THE TIME STEP 38 IS COMPLETED
THE TIME STEP 39 IS COMPLETED
THE TIME STEP 40 IS COMPLETED
THE TIME STEP 41 IS COMPLETED
THE TIME STEP 42 IS COMPLETED
THE TIME STEP 43 IS COMPLETED
THE TIME STEP 44 IS COMPLETED
THE TIME STEP 45 IS COMPLETED
THE TIME STEP 46 IS COMPLETED
THE TIME STEP 47 IS COMPLETED
UX4.035133912111094E-03 9044 -4.962019779499589E-06 8452 7.704656665594700E-06FULLGRD2000
ECRIT(63) 277-UX P 2000 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 967066 3402
UX2.274971188079485E-02 11306 -3.569080791511551E-06 4399 1.063844769090322E-05FULLGRD3400
ECRIT(63) 278-UX P 3400 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 970471 3402
UX1.264558816250615E-02 11305 -5.057743116322687E-06 10007 6.908066294770146E-06FULLGRD6300
ECRIT(63) 279-UX P 6300 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 973876 3402
UX3.682073612016761E-03 11432 -3.174273349914793E-06 9065 4.211273653016348E-06FULLGRD9480
ECRIT(63) 280-UX P 9480 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 977281 3402
UX-1.753870013469004E-03 6710 -5.672262136904163E-06 8930 4.848135557249551E-06FULLGRD11700
ECRIT(63) 281-UX P 11700 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 980686 3402
UX-3.177626293788830E-03 6577 -7.297112161527468E-06 8930 5.015071584586584E-06FULLGRD12000
ECRIT(63) 282-UX P 12000 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 984091 3402
VX-8.761432589326791E-04 10871 -1.413451414066825E-05 9152 8.633409688016218E-06FULLGRD2000
ECRIT(63) 283-VX P 2000 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 987496 3402
VX9.652438139241753E-04 7985 -8.597106336135583E-06 10385 6.170052999156368E-06FULLGRD3400
ECRIT(63) 284-VX P 3400 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 990901 3402
VX8.053641829097145E-04 7718 -7.318014418652936E-06 11037 6.982582994779959E-06FULLGRD6300
ECRIT(63) 285-VX P 6300 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 994306 3402
VX6.922208306190007E-04 8527 -4.328207531074084E-06 9491 4.519316949701795E-06FULLGRD9480
ECRIT(63) 286-VX P 9480 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 997711 3402
VX8.158009592366922E-04 9740 -4.184621512417131E-06 11028 5.080726112853317E-06FULLGRD11700
ECRIT(63) 287-VX P 11700 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 1001116 3402
VX1.415510568805592E-03 9470 -5.114588379793693E-06 6709 5.269872778921766E-06FULLGRD12000
ECRIT(63) 288-VX P 12000 24 0 136 100 1 GEF772 6021293122 1800 48 Z 1 0 1 0 R16 1004521 3402
GO4138848400.281008 12770 283004.4301822601 1890 313206.9534983745FULLGRD2000
ECRIT(63) 289-GO P 2000 24 0 136 101 1 GEF772 6021293122 1800 48 Z 0 0 1 0 R16 1007926 3436
GO1826519139.287095 12752 121522.9932873652 9050 140595.4755748139FULLGRD3400
ECRIT(63) 290-GO P 3400 24 0 136 101 1 GEF772 6021293122 1800 48 Z 0 0 1 0 R16 1011376 3436
GO868474489.2723909 12616 56311.38878271090 9454 67709.04178724089FULLGRD6300
ECRIT(63) 291-GO P 6300 24 0 136 101 1 GEF772 6021293122 1800 48 Z 0 0 1 0 R16 1014826 3436
GO312658296.5220652 12610 19893.64884636139 9184 24871.66923459355FULLGRD9480
ECRIT(63) 292-GO P 9480 24 0 136 101 1 GEF772 6021293122 1800 48 Z 0 0 1 0 R16 1018276 3436
GO33213607.13354784 12748 1978.805145948684 9184 2724.236434006759FULLGRD11700
ECRIT(63) 293-GO P 11700 24 0 136 101 1 GEF772 6021293122 1800 48 Z 0 0 1 0 R16 1021726 3436
GO0.000000opotential height differences (m) of four schemes wrt the
control as a function of timestep (h). Solid - RSR94 (
 );
dash/dot - RSR94 (
);
dash/dot - RSR94 (
 );
long dashed - backward implicit (
);
long dashed - backward implicit (
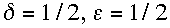 );
short dashed - (
);
short dashed - (
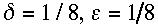 ).
).
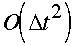 -accurate
schemes, introduced in Rivest et al. (1994) to address the problem of the
spurious resonant response of semi-implicit semi-Lagrangian schemes at large
Courant number, has been generalized to a two-parameter family by introducing
the possibility of evaluating total derivatives using an additional time level.
The merits of different members of this family based on both theory and results
are assessed. The additional degree of freedom might be expected a priori to
permit a reduction of the time truncation errors while still maintaining
stability and avoiding spurious resonance. Resonance, stability and truncation
error analyses for the proposed generalized family of schemes are given. The
sub-family that is formally
-accurate
schemes, introduced in Rivest et al. (1994) to address the problem of the
spurious resonant response of semi-implicit semi-Lagrangian schemes at large
Courant number, has been generalized to a two-parameter family by introducing
the possibility of evaluating total derivatives using an additional time level.
The merits of different members of this family based on both theory and results
are assessed. The additional degree of freedom might be expected a priori to
permit a reduction of the time truncation errors while still maintaining
stability and avoiding spurious resonance. Resonance, stability and truncation
error analyses for the proposed generalized family of schemes are given. The
sub-family that is formally
 -accurate
is unfortunately unstable for gravity modes. Sample integrations for various
members of the generalized family are shown. Results are consistent with
theory, and stable non-resonant forecasts at large Courant number are possible
for a fairly broad choice of values of the two free parameters. Of the two
methods proposed in Rivest et al. (1994) for computing trajectories, the one
using a piecewise-defined trajectory is to be preferred to that using a single
great-circle arc, since it is more accurate at large timestep for some members
of the generalized family.
-accurate
is unfortunately unstable for gravity modes. Sample integrations for various
members of the generalized family are shown. Results are consistent with
theory, and stable non-resonant forecasts at large Courant number are possible
for a fairly broad choice of values of the two free parameters. Of the two
methods proposed in Rivest et al. (1994) for computing trajectories, the one
using a piecewise-defined trajectory is to be preferred to that using a single
great-circle arc, since it is more accurate at large timestep for some members
of the generalized family.
 ,
(2.1)
,
(2.1)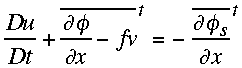 ,
(2.2)
,
(2.2)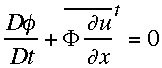 ,
(2.3)
,
(2.3) and
and
 are respectively the fluid depth and orographic height multiplied by
are respectively the fluid depth and orographic height multiplied by
 ,
the other symbols have their usual meaning, and for the generalized
family of schemes introduced here:
,
the other symbols have their usual meaning, and for the generalized
family of schemes introduced here: ,
(2.4)
,
(2.4) ,
(2.5)
,
(2.5) .
(2.6)
.
(2.6) and
and
 are assumed non-zero, and the orographic geopotential
are assumed non-zero, and the orographic geopotential
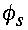 is both non-zero and time invariant. The linearized equations before
discretization may be recovered by redefining
is both non-zero and time invariant. The linearized equations before
discretization may be recovered by redefining
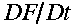 and
and
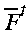 as:
as: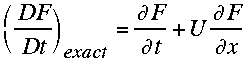 ,
(2.7)
,
(2.7) .
(2.8)
.
(2.8)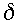 ,
, )
family of schemes is the most general
)
family of schemes is the most general
 -accurate
scheme based on three time levels, and is a generalization of the 1-parameter (
-accurate
scheme based on three time levels, and is a generalization of the 1-parameter (
 )
family presented in RSR94. The parameter
)
family presented in RSR94. The parameter
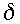 here is exactly as in RSR94. It was introduced there to decenter the
2-time-level Crank-Nicolson semi-implicit semi-Lagrangian discretization, and
thereby address the problem of spurious orogrophically-induced resonance by
introducing a third time level to evaluate the time-averaged contributions
along the trajectory. A further new parameter
here is exactly as in RSR94. It was introduced there to decenter the
2-time-level Crank-Nicolson semi-implicit semi-Lagrangian discretization, and
thereby address the problem of spurious orogrophically-induced resonance by
introducing a third time level to evaluate the time-averaged contributions
along the trajectory. A further new parameter
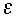 has been added here. It optionally introduces the use of a third time level
in the evaluation of the time derivatives along the trajectory. This
additional degree of freedom might be expected a priori to permit an
improvement to the RSR94 family of schemes by reducing the time truncation
errors [possibly to
has been added here. It optionally introduces the use of a third time level
in the evaluation of the time derivatives along the trajectory. This
additional degree of freedom might be expected a priori to permit an
improvement to the RSR94 family of schemes by reducing the time truncation
errors [possibly to
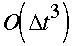 ]
while still maintaining stability and avoiding spurious resonance. This is
discussed further later. Special cases of the above generalized scheme for
particular values of
]
while still maintaining stability and avoiding spurious resonance. This is
discussed further later. Special cases of the above generalized scheme for
particular values of
 and
and
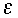 are summarized in Table 1.
are summarized in Table 1.
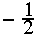 Crank-Nicolson using time levels t and
t-2[[Delta]]t
d 0 General RSR94 1-parameter (d) scheme
Crank-Nicolson using time levels t and
t-2[[Delta]]t
d 0 General RSR94 1-parameter (d) scheme
 0 Particular RSR94 scheme, for which results were
shown
0 Particular RSR94 scheme, for which results were
shown

 Backward implicit
Backward implicit
 and
and
 .
.
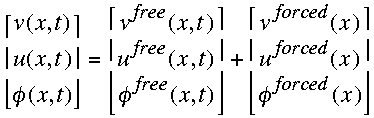 .
(2.7)
.
(2.7)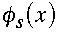 set identically to zero. Letting
set identically to zero. Letting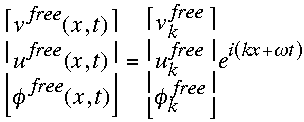 ,
(2.8)
,
(2.8) ,
(2.9)
,
(2.9)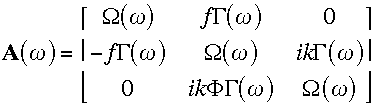 ,
(2.10)
,
(2.10) ,
(2.11)
,
(2.11) ,
(2.12)
,
(2.12)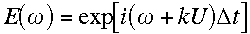 ,
(2.13)
,
(2.13) ,
(2.14)
,
(2.14)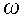 .
Note that for the exact solution of the linearized equations (with no
discretization), (2.11)-(2.12) may be replaced by the definitions
.
Note that for the exact solution of the linearized equations (with no
discretization), (2.11)-(2.12) may be replaced by the definitions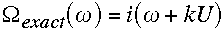 ,
(2.15)
,
(2.15) ,
(2.16)
,
(2.16)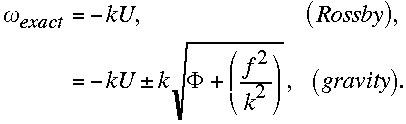 (2.17)
(2.17)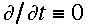 ),
and may be Fourier decomposed as
),
and may be Fourier decomposed as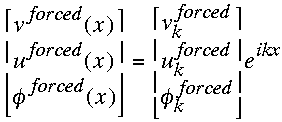 .
(2.18)
.
(2.18) .
(2.19)
.
(2.19) simplifies to
simplifies to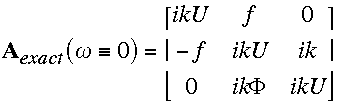 ,
(2.20)
,
(2.20)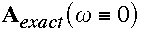 vanishes, i.e. when
vanishes, i.e. when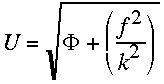 ,
(2.21)
,
(2.21)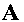 defined by (2.10) plays a determining role for both resonance and stability.
These latter are respectively discussed in the following two sub-sections.
defined by (2.10) plays a determining role for both resonance and stability.
These latter are respectively discussed in the following two sub-sections.
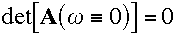 ,
(2.22)
,
(2.22)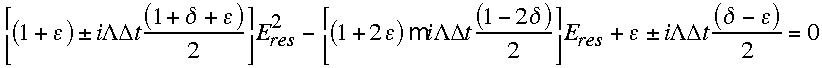 ,
(2.23)
,
(2.23)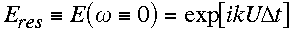 ,
(2.24)
,
(2.24)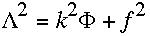 .
(2.25)
.
(2.25) is real by definition, resonance is only possible if
is real by definition, resonance is only possible if
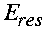 lies on the unit circle, i.e. if
lies on the unit circle, i.e. if .
(2.26)
.
(2.26)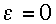 ,
the conditions (2.23) for resonance in the present 2-parameter (
,
the conditions (2.23) for resonance in the present 2-parameter (
 )
family of schemes reduce to (15) of RSR94 for their 1-parameter (
)
family of schemes reduce to (15) of RSR94 for their 1-parameter (
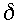 )
family. The further special case
)
family. The further special case
 (cf. Table 1), corresponds to the conditions (9) of RSR94 for the spurious
resonance of centered 2-time-level semi-implicit semi-Lagrangian schemes. As
discussed in RSR94, spurious resonance occurs for certain combinations of large
Courant number and nondimensional wavenumbers of the orographic forcing, and
can be avoided by suitably off-centering the time discretization along the
trajectory. In the present study this is controlled by the
(cf. Table 1), corresponds to the conditions (9) of RSR94 for the spurious
resonance of centered 2-time-level semi-implicit semi-Lagrangian schemes. As
discussed in RSR94, spurious resonance occurs for certain combinations of large
Courant number and nondimensional wavenumbers of the orographic forcing, and
can be avoided by suitably off-centering the time discretization along the
trajectory. In the present study this is controlled by the
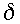 and
and
 parameters.
parameters.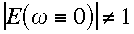 .
They may not however necessarily be stable, and this aspect of the
discretization is examined in the following sub-section.
.
They may not however necessarily be stable, and this aspect of the
discretization is examined in the following sub-section.
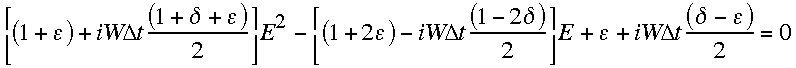 ,
(2.27)
,
(2.27) ,
(2.28)
,
(2.28) ,
(2.29)
,
(2.29) .
(2.30)
.
(2.30)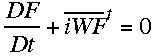 ,
(2.31)
,
(2.31)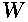 is real. This is equivalent to having performed a decomposition in terms of
the eigen-functions of the matrix
is real. This is equivalent to having performed a decomposition in terms of
the eigen-functions of the matrix
 .
The leading-order term of the truncation error (placed on the right-hand side
of 2.31) is
.
The leading-order term of the truncation error (placed on the right-hand side
of 2.31) is .
(2.32)
.
(2.32) ),
(2.27) factors easily and
),
(2.27) factors easily and
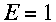 or
or
 .
The first root corresponds to the physical Rossby mode and it is stable since
it satisfies (2.30). The other root corresponds to a computational Rossby mode
(introduced by discretizing a 1st-order-in-time equation over three time
levels), and it will satisfy (2.30) and be stable provided
.
The first root corresponds to the physical Rossby mode and it is stable since
it satisfies (2.30). The other root corresponds to a computational Rossby mode
(introduced by discretizing a 1st-order-in-time equation over three time
levels), and it will satisfy (2.30) and be stable provided
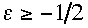 .
Now
.
Now
 corresponds to a centered three-time-level discretization, and this value for
corresponds to a centered three-time-level discretization, and this value for
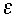 must be excluded since (see above and RSR94) the stationary forced gravity
modes would suffer from spurious resonance. Although satisfaction of the
strict inequality
must be excluded since (see above and RSR94) the stationary forced gravity
modes would suffer from spurious resonance. Although satisfaction of the
strict inequality
 is sufficient to stabilize the computational Rossby mode,
is sufficient to stabilize the computational Rossby mode,
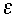 should be positive, otherwise it will have the undesirable property of changing
the sign of this computational mode at alternate timesteps (timestep
decoupling).
should be positive, otherwise it will have the undesirable property of changing
the sign of this computational mode at alternate timesteps (timestep
decoupling).
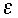 should not only be positive but small to ensure adequate damping of this
computational mode during the integration.
should not only be positive but small to ensure adequate damping of this
computational mode during the integration. 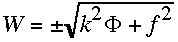 ),
(2.27) does not factor easily. It is nevertheless possible to get some insight
into the influence of
),
(2.27) does not factor easily. It is nevertheless possible to get some insight
into the influence of
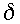 and
and
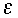 on the stability of the free gravity solutions by solving (2.27) asymptotically
for
on the stability of the free gravity solutions by solving (2.27) asymptotically
for
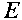 for the physical mode when
for the physical mode when
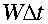 is small. Taking its modulus then gives
is small. Taking its modulus then gives .
(2.33)
.
(2.33)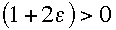 for stability of the computational Rossby solution, it is necessary to take
for stability of the computational Rossby solution, it is necessary to take ,
(2.34)
,
(2.34) -accurate member of the present generalized family of three-time-level schemes
(i.e.
-accurate member of the present generalized family of three-time-level schemes
(i.e.
 )
is unstable and therefore inadmissible. This is unfortunate. By numerically
solving (2.27) when
)
is unstable and therefore inadmissible. This is unfortunate. By numerically
solving (2.27) when
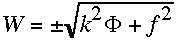 for a broad range of values of the parameters
for a broad range of values of the parameters
 ,
,
 ,
and
,
and
 ,
it is found that the valid domain for remaining both stable and off resonance
is
,
it is found that the valid domain for remaining both stable and off resonance
is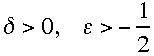 ,
(2.35)
,
(2.35) and
and
 from the more restricted domain
from the more restricted domain ,
(2.36)
,
(2.36) and
and
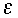 (consistent with being adequately off-resonance), to respectively minimize the
truncation errors (see 2.32) and to maximally damp the computational Rossby
mode.
(consistent with being adequately off-resonance), to respectively minimize the
truncation errors (see 2.32) and to maximally damp the computational Rossby
mode.
 )
)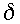 and
and
 ,
the methodology introduced in RSR94 is adopted. The grid configuration and the
model orography used here are as depicted in their Figs. 4 and 5. The grid has
a uniform (
,
the methodology introduced in RSR94 is adopted. The grid configuration and the
model orography used here are as depicted in their Figs. 4 and 5. The grid has
a uniform (
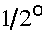 )
resolution window over N. America, and the orography is zero everywhere outside
this window. The experiments consist of 48-h forecasts initiated from the
500hPa height and wind analyses of 1200 UTC 12 February 1979 after an
implicit-normal-mode initialization. The initialized geopotential used in all
of the described experiments is displayed in Fig. 6 of RSR94.
)
resolution window over N. America, and the orography is zero everywhere outside
this window. The experiments consist of 48-h forecasts initiated from the
500hPa height and wind analyses of 1200 UTC 12 February 1979 after an
implicit-normal-mode initialization. The initialized geopotential used in all
of the described experiments is displayed in Fig. 6 of RSR94. is obtained as in Côté et al. (1993) using winds extrapolated
forward from those at ess the problem of the spurious resonance of
semi-implicit semi-Lagrangian schemes at large Courant number, has been
generalized to a two-parameter three-time-level family by introducing the
possibility of evaluating total derivatives using an additional time level of
information. The RSR94 family can be considered to be the limiting case of the
generalized family that maximally simplifies the evaluation (using a
two-time-level difference) of the total derivatives. The other limiting case
is the "backward-implicit" scheme, where maximum simplification of the
evaluation (entirely at the arrival point) of the other terms occurs, and where
an additional (third) time level is employed to evaluate the total derivatives.
It has the virtues that the only upstream evaluations required are those
associated with the total derivatives, and that it does not require derivative
terms such as
is obtained as in Côté et al. (1993) using winds extrapolated
forward from those at ess the problem of the spurious resonance of
semi-implicit semi-Lagrangian schemes at large Courant number, has been
generalized to a two-parameter three-time-level family by introducing the
possibility of evaluating total derivatives using an additional time level of
information. The RSR94 family can be considered to be the limiting case of the
generalized family that maximally simplifies the evaluation (using a
two-time-level difference) of the total derivatives. The other limiting case
is the "backward-implicit" scheme, where maximum simplification of the
evaluation (entirely at the arrival point) of the other terms occurs, and where
an additional (third) time level is employed to evaluate the total derivatives.
It has the virtues that the only upstream evaluations required are those
associated with the total derivatives, and that it does not require derivative
terms such as
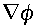 and
and
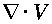 to be evaluated at any time other than the present one (which is done
implicitly and only at arrival meshpoints). Both of these limiting cases are
off-centered discretizations, to avoid spurious resonance, and all schemes
examined are
to be evaluated at any time other than the present one (which is done
implicitly and only at arrival meshpoints). Both of these limiting cases are
off-centered discretizations, to avoid spurious resonance, and all schemes
examined are
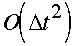 accurate.
accurate. ,
,
 );
); and
and
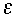 from the more restricted domain (
from the more restricted domain (
 ,
,
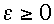 ),
to avoid having a time-decoupled computational Rossby mode;
),
to avoid having a time-decoupled computational Rossby mode; and
and
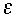 (consistent with being adequately off resonance), to respectively minimize the
truncation errors and to maximally damp the computational Rossby mode;
(consistent with being adequately off resonance), to respectively minimize the
truncation errors and to maximally damp the computational Rossby mode;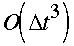 -accurate
(
-accurate
(
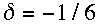 ,
,
 free), it is unstable for the gravity modes; this is unfortunate; starting from
a stable-but-resonant centered two-time-level scheme (
free), it is unstable for the gravity modes; this is unfortunate; starting from
a stable-but-resonant centered two-time-level scheme (
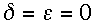 ),
a degree of freedom can be added to address resonance (by using an additional
time level and thereby decentering either the evaluation of the total
derivatives or the other terms), but adding a further degree of freedom (while
still only using three time levels) does not permit increasing accuracy to
),
a degree of freedom can be added to address resonance (by using an additional
time level and thereby decentering either the evaluation of the total
derivatives or the other terms), but adding a further degree of freedom (while
still only using three time levels) does not permit increasing accuracy to
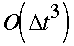 .
.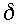 and
and
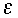 parameters. Within the RSR94 family of schemes, the scheme (
parameters. Within the RSR94 family of schemes, the scheme (
 )
for which results were shown in RSR94 is a good choice but not an optimal one.
A smaller value of
)
for which results were shown in RSR94 is a good choice but not an optimal one.
A smaller value of
 than 1/2, but no smaller than 1/6, can reduce the leading-order term for the
truncation error by as much as a factor of 2 (see 2.32) and the damping rate by
as much as a factor of 3 (see 2.33), while still acceptably controlling
resonance. Finally, it was found that while either of the two methods
presented in RSR94 for computing the trajectories is acceptable for their
scheme, only one of them is acceptable at large timestep for some members of
the generalized family. The method that computes the trajectory in a piecewise
fashion is therefore to be preferred to the one that uses a single great-circle
trajectory.
than 1/2, but no smaller than 1/6, can reduce the leading-order term for the
truncation error by as much as a factor of 2 (see 2.32) and the damping rate by
as much as a factor of 3 (see 2.33), while still acceptably controlling
resonance. Finally, it was found that while either of the two methods
presented in RSR94 for computing the trajectories is acceptable for their
scheme, only one of them is acceptable at large timestep for some members of
the generalized family. The method that computes the trajectory in a piecewise
fashion is therefore to be preferred to the one that uses a single great-circle
trajectory.
 )
with
)
with
 =10 min.
=10 min.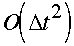 "backward-implicit" scheme (
"backward-implicit" scheme (
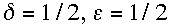 )
with
)
with
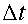 = 60 min.
= 60 min.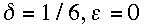 )
with
)
with
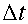 = 60 min.
= 60 min. );
dash/dot - RSR94 (
);
dash/dot - RSR94 (
 );
long dashed - backward implicit (
);
long dashed - backward implicit (
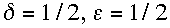 );
short dashed - (
);
short dashed - (
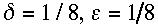 ).
).